2021학년도 수능 가형 20번 어려운 이유 & 해설
게시글 주소: https://orbi.kr/00033501365
2021학년도 수능 가형 20번 (by.csm).pdf
안녕하세요 CSM입니다.
20번 해설을 들고왔습니다.
현재 21번보다
체감 난이도가 높다고 여겨지는 20번입니다.
21번
체감난이도가 높은 이유는
1) 함수 g(x)의 치역설정
2) 정적분의 "결과값"을 통해 함수 개형추론
에 있어서 기존 기출에서
단단하게 연습하기 어려운 형태여서
학생들이 조금 풀기 어려워한 듯 보입니다.
먼저 교양적으로 알아야 할 사실은
아래 그림과 같이 삼각함수 반주기의
넓이(정적분값)를 빠르게 파악해야 합니다.
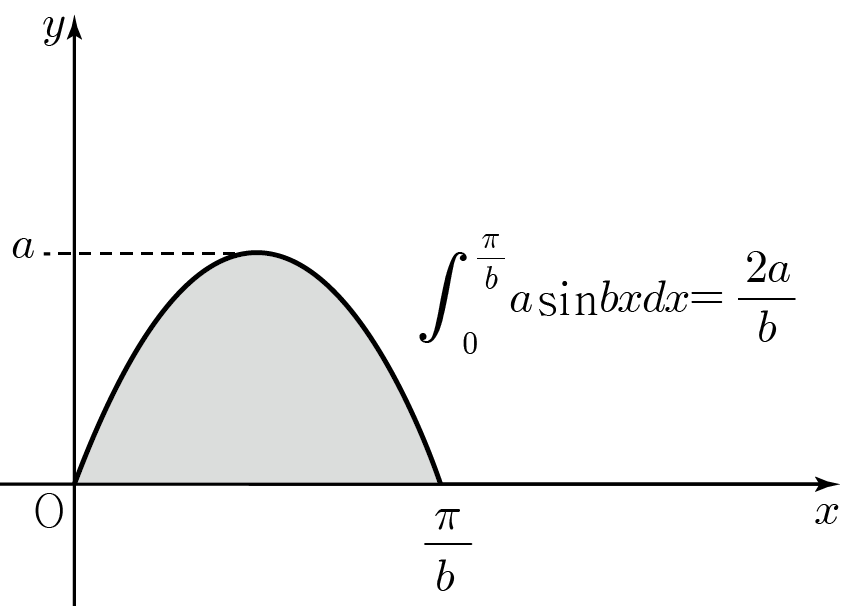
이를 토대로 해설은 다음과 같습니다. (아래 이미지 PDF도 첨부)
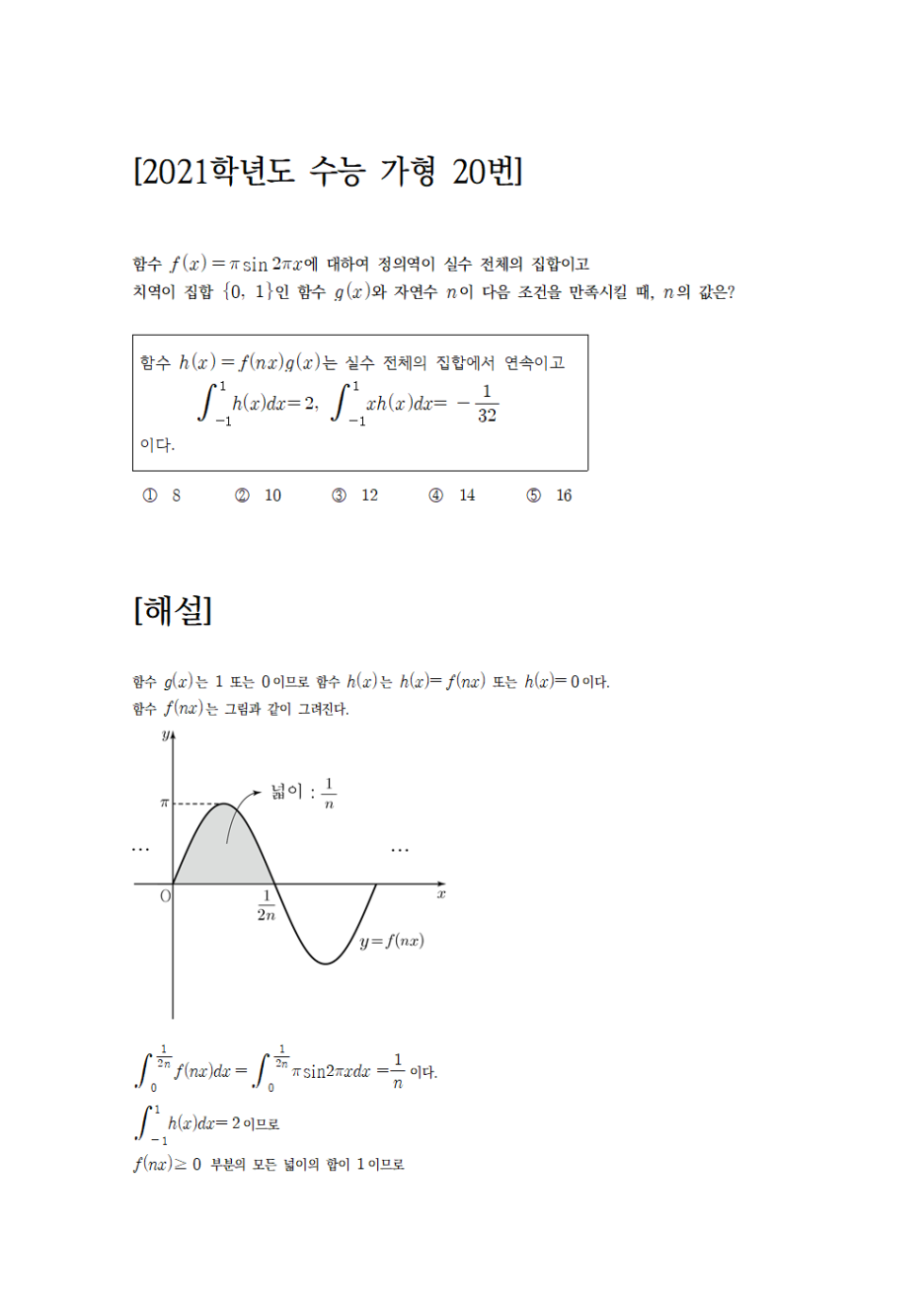
사진 설명을 입력하세요.
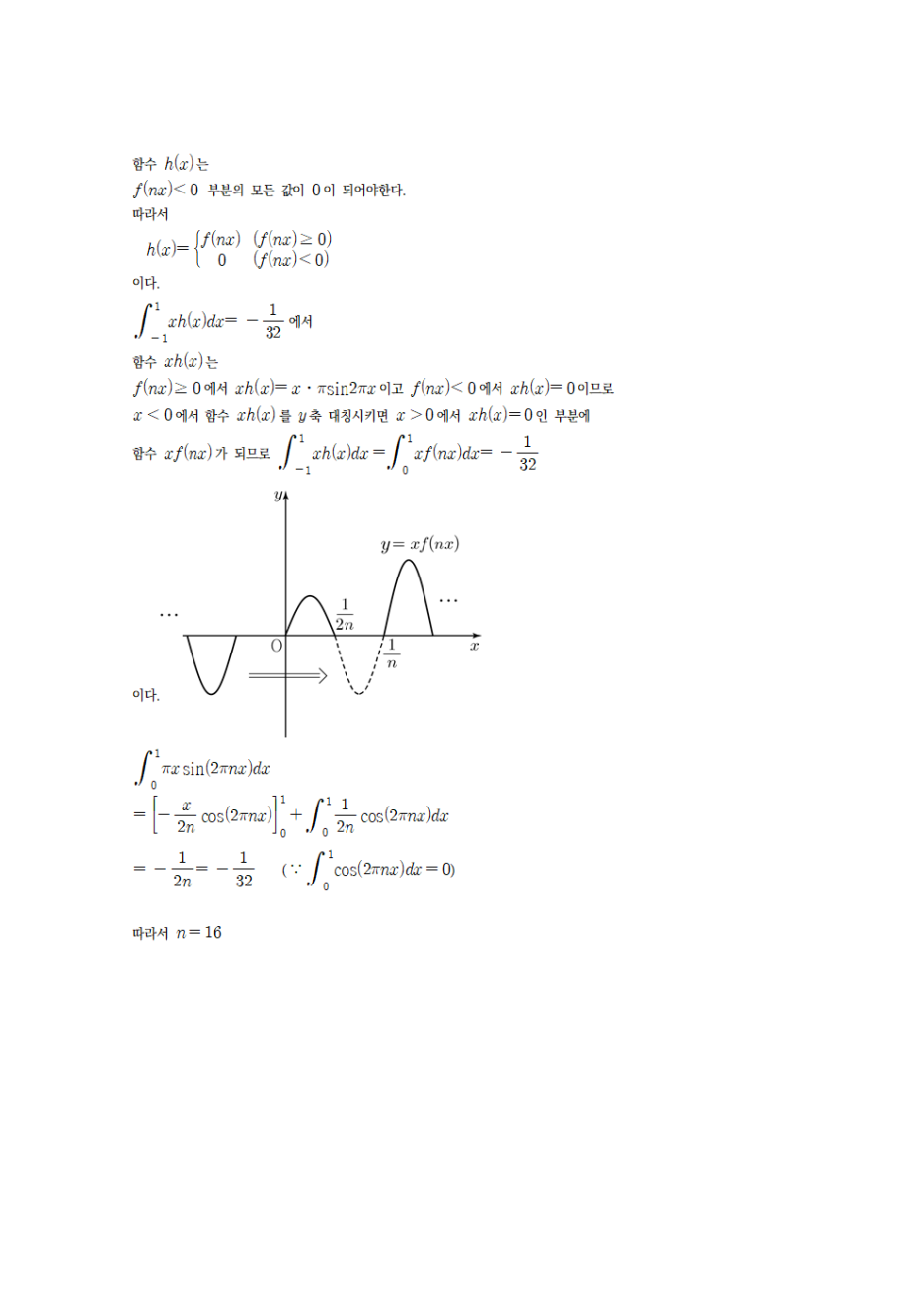
사진 설명을 입력하세요.
두가지 적분의 해석을 넓이관점과 식의 관점으로 보는 방향에 따라
풀이속도가 달라질 수 있는 문제이고 이런 경우에는
학생들에게 체감난이도 격차를 줄 수 있었던 문제라고 생각합니다.
도움이 되셨기를 바랍니다.
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
첫 정답자 2000덕 드리겠습니다!
-
흑흑 또 고추밭이야
-
2차도 쳐야될 거 같네요.. 검정고시 오전 정답
-
제 1대 인민주석총통권한대행 이재명
-
션티 선생님이 서평을 써주신 수능 영어 책이 있다?!?! 3
https://atom.ac/books/13231/ ㄷㄷ '수능영어란 표면(A)이...
-
6일 전부터 투표 마감 시각 사이에 여론조사 결과 보도하면 젖지한테 독포먹나요
-
ㅈㄱㄴ 에센스는 또 뭐냐
-
다른 가능성이 있긴하나요 다 컷 계산해서 넣는건데
-
작년에 콘서타 5개월정도 먹었었는데 이번에는 약안먹고 몯스터 먹으명서 하려는데
-
국어 수학 다 김범준으로 하는 중 국정원 범작가 스블 김범준 물리도 가끔 범물리 들음(물론 김범준)
-
일요일에 평소 루틴대로 안하고 하고 싶은 과목 공부해도 될까요
-
지인선 n제 1
첫 N제로 이거 풀어보는중인데 항상 2개에서 많으면 4개정도 못풀어요 근데 문제는...
-
굳이 할거면 한 5월말에 해라
-
몸이 쓰레기야
-
6시에 올게요 1
-
팀수업 시간인데 5
스카에 아무도 안 옴 왜 다 늦냐...
-
6월3일 조기대선? “고3 모의고사와 겹쳐”..교육계 촉각[윤 대통령 파면] 4
[파이낸셜뉴스] 윤석열 대통령 파면으로 조기 대선이 확정된 가운데 정치권에서...
-
그리고 이 Arbor은 라틴어 herba에서 온 말로 허브(herb)와 동원
-
근데 그러면 특정당할 위험이 있기에...
-
날씨가 개지랄 중이라 사기가 귀찮다 반팔티 서너개랑 반팔셔츠 하나 버뮤다 팬츠...
-
오르비에 또 2
오르비에또
-
조금 만 더 화이팅! 오늘 시험 보신분들 채점하세요~ ▶ 검정고시 정답 확인
-
뿌우
-
AI는 신이야 0
AI 덕에 내 인생이 배로 쉬워졌다
-
하의대 보내달라고
-
사탐으로 광역 들어가서 공대로 졸업 가능?
-
나는 친구랑 게임얘기만 하는데 선지 뭐 골랐어? 공부얘기하니까 너무부럽다
-
엄기은 deep 0
솔텍이랑 비교했을때 난이도 어떤가요?
-
4시간 늦게온다고 통보했어요 Wa! 학생정신주입봉 만들어야겠음
-
개념부분은 충분하다고 생각하고 도표 엠스킬 돌리고있습니다 빨더텅으로 실전연습 겸...
-
미션중
-
수학1 한완기 풀고 있는데요... 답은 맞긴하는데 제 풀이가 해설지 풀이보다 약간...
-
만년필도 이쁘고 시계도 이쁘고 지갑도 이쁜 우리 몽블랑
-
이거 어떻게 해결하나요 제발 알려주세요
-
고2 정파는 일년이 나무 붕뜨는거 같아요
-
시발내샤프가 12
고2때부터 함께해온 그래프1000을 방금 떨어뜨렸는데 사망했음
-
1시 수업인데 0
밥도 못 먹었네 오르비할려고했는데
-
아 3
오
-
내 초밥 언제와아아아악 12
생선을 주문 받고 잡으러 간거임??
-
이걸 어케 풀어요 ㅎㅎ
-
수특 문학 변형문제집 추천해주세요
-
진짜 개힘드네
-
맥도날드 버거 한번 먹어보자
-
잘 살고싶은데 1
세상이 호락호락하지 않네..
-
지피티보다 훨씬 피뎁 정리가 자세하다
-
으악 비가 와 7
비 맞은 채로 과외 가기 꼬질꼬질하군
-
필청명반 2
들어라.
-
연예인 기획사에서 단체로 검고 응시라도 시켰나
-
저는 여기서 봤어요 남은 시간도 화이팅! ▶검정고시 답안 확인





















































개인적으로 매우 친숙한 유형은 아니라고 생각합니다. 현장기준 어려웠을 것 같아요
asinbx 한칸넓이 a/b라서 n이 2의거듭제곱만 될거같아서 1.5중에 고민하고 5번 왼쪽정적분으로 계산해보니 사인 양수는 0곱해서 없어질것같고 음수는 -1곱해져서 양수가 될것같은 느낌으로 킹리적갓심씀
ㄹㅇ 걍 찍맞이네
아니에요 킹리적갓심은 절대 그냥 나오지 않습니다. 잘하셨습니다 ^__^
해설 잘 봤어요. 마지막에 정적분 int_{-1}^{1} xh(x)dx=int_{0}^{1} xf(nx)로 넘어가는 부분이 잘 이해가 안되는데 혹시 여유있으시다면 설명해주실 수 있을까요? 저는 사진처럼 풀었는데, 계산이 무척 더럽고 현장에서 저렇게 풀면 계산실수가 반드시 있을 것 같아서 부탁드립니다....(첫 줄의 오류는 건너뛰어주세요 고치기 귀찮아서...ㅎㅎ)
in_{-1}^{0}xh(x)dx 부분만 관찰해주시면 될 것 같습니다. 함숫값이 음수인 부분은 제거 되었을것이고 양수인부분만 남은 h(x)에 대하여 x를 곱하는데 x<0이므로 xh(x)<0가 됩니다.
따라서 xh(x)를 (-1,1)에서 그린 후 각각 적분을 하여도 괜찮습니다만,
(-1,0)인 부분을 그대로 y축 대칭시켜보면 결국 xf(nx)가 완성된다는 것을 알 수 있습니다.
이는 f(nx)가 처음부터 대칭함수이고 x를 곱하여서 '대칭성질'이 남아있다고 생각하여 판단할 수 있으며 이를 (-1, 0) => (0, 1)로 이동하는 치환적분하여 식적으로도 설명가능하나 이를 계산으로 의도하기보다는 최근 "영역관찰"을 포인트 잡아왔기에 그림도 적절히 섞어서 확인해주시면 될 것 같습니다.^^
아아아아 다 그대로 대칭되니까 그렇겠네요 감사합니다.
찍는게 더 빠를 듯. 2랑 1/32 나오고 f(nx) 주기가 1/n 이니까 8, 16 처럼 2의 거듭제곱꼴로 나오는 수가 답일 것 같고 8은 너무 작아서 16했는데 아.. 계산이 엄청 빡센거였네요
진짜 시험장에서 제일 어려웠어요... 30 20 이 최고봉.
이제 21 29 은 킬러 아닌듯해여ㅜ
와.. 그냥 1/2n~1/n, 1/n~3/2n 계속 적분해가면서 귀납적으로 적분값을 찾아냈는데 y축대칭하면 한번의 적분으로 풀리네요 진짜 충격이네